{youtube}Baobz1QupVs{/youtube}
THE MAGIC PROPERTIES OF CARBON FOR QUANTUM COMPUTING
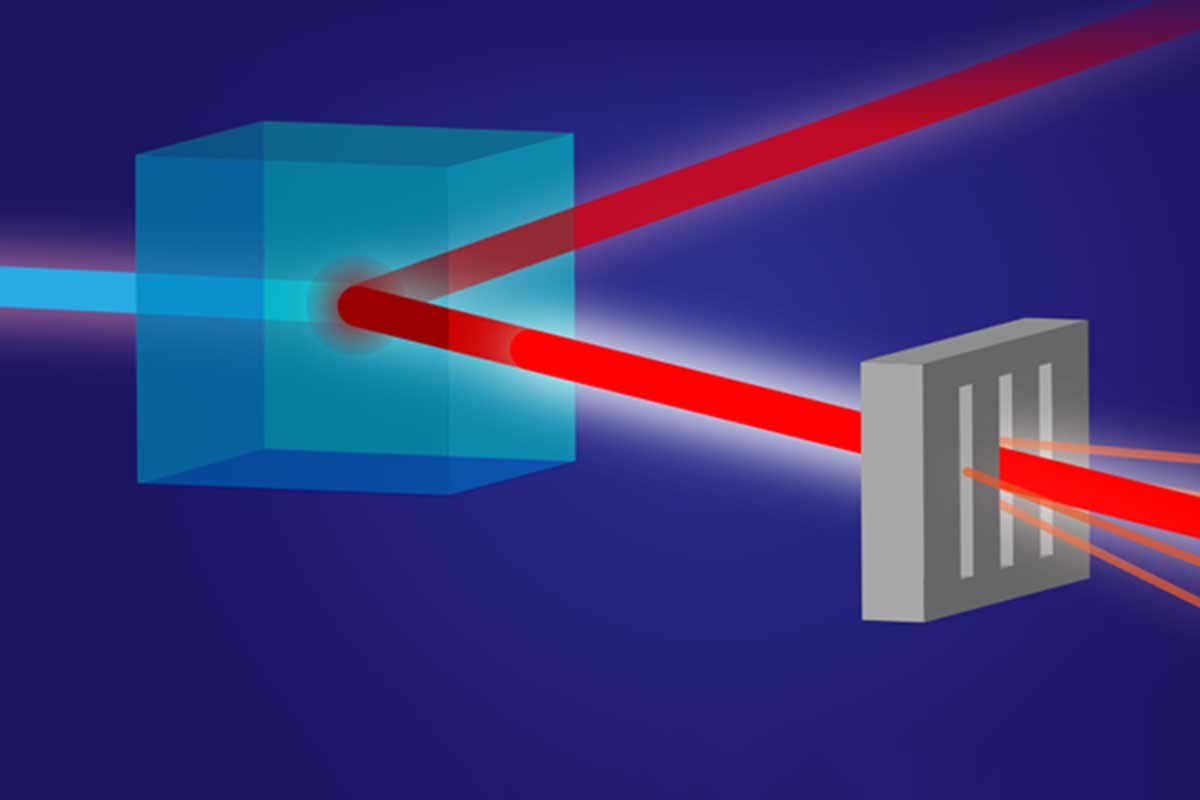
An article in New Scientist Quantum X-ray machine takes razor sharp pictures with less radiation explains how to split X-rays by passing them thru a diamond and then they can use the entanglement properties of quantum particles so that the photons in one stream will have the same quantum properties as photons in the other streams. They do this by directing the X-rays thru a diamond which is pure carbon. In my video above How to make a quantum computer I explain how the DNA is essentially made up of carbon interspersed with hydrogen nitrogen and oxygen atoms. The point is that the DNA presents essentially as a carbon based semi-conducting nanowire. It is suggested that this new research of splitting X-rays by shining them thru a diamond is essentially the same process as what is occurring in the DNA where biophotons (UV and visible light) are being split and redirected as part of quantum computing processes. https://www.newscientist.com/article/2214790-quantum-x-ray-machine-takes-razor-sharp-pictures-with-less-radiation/
Post in Quantum Computing group on Facebook 1st March, 2019.
It’s just dawned on me the striking similarities between the ‘two-slits’ experiment and the DNA Phantom Effect. They both involve an experimenter shining light thru an apparatus and observing the wave pattern that appears on a screen behind. In other words they both involve this fundamental mystery of wave-particle duality. I have just realized that in both experiments we actually get to ‘see’ the probability waves of QM. When you think of it all the wave theory of light based on Fourier maths is in the nature of probability waves. The wave nature of light is what ‘probably’ happens and then miraculously when you observe a photon you find wonder of wonders that is what actually happens. For instance photons don’t spread out in all directions from a bright orb billions of light years away and then travel indefinitely in perfectly straight lines sinusoidal oscillating from -1 to +1 on a Cartesian grid with no mass and no energy thru a void and then arrive in perfectly parallel ‘rays’ into the retina of our eyes so we see a perfectly coherent bright orb. Real physical photons would surely be no longer parallel and would be entering our eyes at an angle and should have spread out. I could list another dozen mysteries about light, The bottom line is ‘wave-particle’ duality mystery is precisely mysterious because we actually ‘see’ the probability waves of QM (if the experimenter doesn’t make an observation then the probability waves travel thru both slits). And in the same way the DNA Phantom Effect is ‘nature’ enabling us to ‘see’ that the probability waves of QM are also occurring in the DNA.
Post in Quantum Computing group on Facebook on 2nd March, 2019
This entanglement experiment in New Scientist raises some interesting questions for quantum computing. Two entangled photons were sent off to labs AO and BO. They were measured by another set of entangled photons AOTest and AOSystem and BOTest and BOSystem. Then the original photon and the AOSystem photons sent on to lab A1 and other original photon and BOSystem sent to lab B1. Researchers claim the observer at AI got different results from ‘observer’ at AO and observer at B1 got different results from ‘observer’ at BO. In fact the ‘observer’ at AO and BO was not a conscious experimenter and the conscious experimenter at A1 and B1 was either choosing randomly to measure either the original photon or the A1System or B1System and the conscious experimenter at A1 and B1 got consistent ‘results’ with each other in as much as they significantly differed from the measurements of the ‘observer’ at AO and BO. All this proves in my opinion is that there is only one measurement within the meaning of QM at the end of process. Presumably in quantum computing there will be an infinitely large number of interactions like this between entangled photons before some sort of a ‘result’ appears on the screen. If the assumption made in this experiment were correct that an observation within the meaning of QM occurs every time there is an interaction between two photons such that the state of one photon changes the state of the other and the result of that ‘observation’ can disagree with ‘observations’ further down the line then you may as well close up shop right now cos quantum computing will never be possible. What would have been startling if the A1 results were 100% consistent with the AO ‘results’ and the B1 results diverged significantly from the BO ‘results’. Then we would have to demolish the Copenhagen school and poor old Niels Bohr would turn over in his grave.
Post in Quantum Computing group on Facebook on 2nd March, 2019.
Well I’ve figured out this question of ‘probability’ waves in light within the meaning of quantum mechanics. Light occupies a unique position in as much as a single photon is clearly a ‘particle’ within the meaning of quantum mechanics and yet we can actually see light thru our sense of vision in the macroscopic world. In other words we do not need a measuring instrument so see light. So in the macroscopic world Fourier wave mechanics apply which will predict how light travels with 100% probability. It is not necessary to square the Fourier integral with it’s complex conjugate (Dirac’s <BRA KET> in order to get a ‘real’ probability and nor is it necessary to normalize the integral. Because the probability waves in the normal Earth based macroscopic world have 100% probability they ‘appear’ real. You can actually see them and predict them with certainty. Then comes Special Relativity and most especially the position of the observer. Special relativity states the probability that objects travelling near speed of light will appear different to a stationary observer here on Earth. It also predicts that the clocks will stop in an object travelling at the speed of light. So to an observer here on Earth it will appear that light from a distant galaxy has taken 10 billion light years to get here according to Fourier wave mechanics, but from the point of view of the photon itself time is simply not a factor. From the point of view of the photon itself it has traversed those 10 billion light years of space instantly and it is as young and as fresh as the instant it was emitted. When it comes to observing photons in the microscopic quantum world, that is to say photons that we can’t actually ‘see’ and now need a measuring instrument to give us a result, then quantum probability rules now apply. I puzzled over that finding that light slows down to 15 miles an hour in a Bose-Einstein condensate. What does that even mean? Light travelling at 15 miles an hour. Then I realized that they didn’t actually ‘see’ the light travelling at 15 miles an hour. There was a probability wave within the meaning of QM that told them the probability that light would travel at 15 miles an hour at near absolute zero and there was a measuring instrument that gave them that ‘result’. The point I’m trying to make is that all wave theory about light are probability waves. But different probabilities apply depending on where you are and what you’re trying to do. I think anyone trying to build a quantum computer in a Bose-Einstein condensate will have to factor this in.
Post in Quantum Computing group on facebook on 2nd March, 2019.
Sorry to be doing all these posts but I got quite a bit to say and if you make these posts too long nobody reads them. For my first post we need a definition of entangled photons. These are photons for which, from their own point of view, no time has passed. Even if they are sent to the two ends of the universe from their own point of view no time has passed. So in that experiment the original entangled photons went from their generation point to labs AO and BO and on to labs A1 and B1 and from their own point of view no time passed and the only measurement took place at labs A1 and B1 and those measurements would have been identical. At labs AO and BO a new set of entangled photons were generated, a test photon and a system photon and the system photon was then sent on with the original photon. Also from the point of view of the system photon no time has passed. The only point in the whole system where time passes is the minuscule amount of time to generate the test and system photons. So the system photon is ever so slightly out of phase with the original photon. From the point of view of all photons no time has passed but when the measurements were made by the conscious observers at labs A1 and B1 their measurements differed slightly from hypothetical measurements that would have been made at labs AO and BO. The point being that there was no observation and no measurement at AO and BO by a conscious experimenter so in the system there was only one point of view – the point of view of the entangled photons themselves and for them no time had passed. The fact that the system and original photons are slightly out of phase only becomes a factor when the measurement is made by the conscious observer and that is why they got a slight discrepancy in results. We can now solve quickly the second issue. The photons operating in a quantum computer in a Bose-Einstein condensate only have their own point of view so for them no time passes cos they’re travelling at the speed of light. They’ll do what they do instantaneously. But if a conscious observer decided to open the can and measure the speed of those photons, the measurement would show that they’re travelling at 15 mph.
Post in Quantum Computing group on Facebook on 3rd March, 2019.
Before someone says to me wait a minute there are lots of particles that are entangled that aren’t travelling at the speed of light I’m gonna head you off at the pass. Photons play out in the macroscopic world so you need an explanation for entanglement of photons in standard physics and that’s special relativity. Atomic and subatomic particles that are entangled don’t need an explanation cos they just form part of a multiparticle wave function and when you collapse the wave function to observe one of them you will automatically get the state of the other. That’s just standard Copenhagen. I think in a quantum computer you will need both forms of entanglement. For instance you generate highly polarized (horizontal or vertical) laser entangled photons one of which reads the data and the other manipulates the nucleus of the hydrogen atom as well as pushing the electron of the hydrogen atom into the conduction band. When that electron falls back into its hole it will emit a single spectral line photon which will read precisely whether that electron is up or down. I think the laser light manipulating the nucleus and reading the data has to be polarized horizontal or vertical cos they constitute orthogonal vectors that will read 0 or 1 (up or down spin). And I think you’re gonna be able to use the DNA molecule itself as the semiconductor. It’s my belief that visible laser light will push the hydrogen electron only into the conduction band. So all you gotta do is direct the laser light at eight hydrogen atoms in the DNA molecule and you will get a reading in spectral line photons of an 8 bit binary number.
Post in Quantum Computing group on Facebook on 5th March, 2019.
In previous posts I described how I thought you can make a quantum computer by generating two entangled laser photons one of which could read the input data and the other is directed at 8 hydrogen atoms that would then emit spectral lines of an 8 bit binary number. In other words this would be a solitonic (solitary) wave packet consisting of 8 spectral lines that contains an 8 bit binary number. This soliton would have non-adiabatic non-abelian geometric phase that contains information. This could then go thru these holonomic quantum gates that would execute some sort of algorithm or program. It would be a very nice concept if at the end of that process the geometric phase of that soliton has been changed into a different 8 bit binary number that represents the result. It’s my feeling that a quantum computer must execute an algorithm or a program instantaneously like Shor’s algorithm. I don’t see how you could have RAM in the conventional sense in a quantum computer. If you’ve followed my ravings up to now one more crazy thought won’t hurt. I’ve got this crazy notion that that result is still entangled with the other laser photon that read the input data and it now changes the hard drive data. The only way this could be justified is if the entire computing process represents a wave function that does not actually collapse until a result appears on the screen for a conscious human computer geek to read and that computer geek actually forms part of the wave function as well. In other words a quantum computer conceptually is just a very sophisticated measuring instrument. All the mysteries that apply to measuring conventional quantum processes will also apply to that quantum computer. You will think I am crazy but Niels Bohr would be proud of me!
Post in Quantum Computing group on Facebook on 8th March, 2019.
“One can recover the information dropped into the black hole by doing a massive quantum calculation on these outgoing Hawking photons,” said Norman Yao, a UC Berkeley assistant professor of physics.
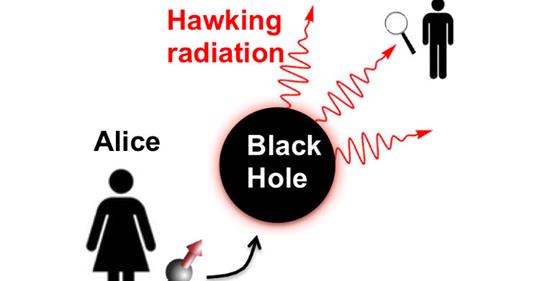
<The trans-Planckian problem is the issue that Hawking’s original calculation includes quantum particles where the wavelength becomes shorter than the Planck length near the black hole’s horizon. This is due to the peculiar behavior there, where time stops as measured from far away. A particle emitted from a black hole with a finite frequency, if traced back to the horizon, must have had an infinite frequency, and therefore a trans-Planckian wavelength.>
This raises some nice issues about my new hobby horse about the probability waves of light. We’ll take this as a pure thought experiment and assume that Einstein’s field equations accurately reflect the fabric of space-time and inside that black hole there is some sort of 4-dimensional milieu that’s accelerating. (the field equations are double differential equations) We drop a 3-D qubit that is stationary in there and then we measure the ‘outgoing Hawking photons’ that is to say we make an observation which collapses a wave function and we observe a photon in a particular state of polarization. We are entitled to surmise that that accurately reflects whether the 3-D qubit is now spin-up or spin-down in the 4-D space-time milieu. If nothing else it reflects the probability waves of all of physics. It’s no more ‘improbable’ than the theory that light travels 13.5 billion years using 3-D Fourier wave mechanics at a constant speed thru 4-D space-time that is accelerating, and that this actually gives us the dimensions of a real physical universe.
Post in Quantum Computing group on Facebook 10th March, 2019
“and it’s probable that there is some secret here which remains to be discovered” quote by C.S. Pierce at head of Eugene Wigner’s article The Unreasonable Effectiveness of Mathematics in the Physical Sciences. I don’t think you are going to make a quantum computer without discovering that ‘secret’. And the secret is (drum roll) all of calculus is in the nature of probability waves whether in the macroscopic or the quantum world. By virtue of Planck’s constant we know that all of matter is composed of discreet chunks ie. all of the physical world is discontinuous. Yet so much of physics involves differentiating waves that are ‘real’ and can’t actually be differentiated because they are discontinuous. Once you realize that all of calculus involves probability wave functions and the only difference between quantum and macroscopic waves is the latter have 100% probability and therefore appear real, then we solve the ‘observation’ question in quantum mechanics. The fact is all of the ‘physical sciences’ require an ‘observer’. A scientist comes up with a hypothesis, does the math, then goes and ‘observes’ whether the hypothesis is true or false. Scientists don’t realize that the ‘observation problem’ applies in the macroscopic world because they have collapsed a wave function that has 100% probability of predicting the outcome of the observation.
